Pullback diagram(1)
If \(\mathcal{J}\) is presented by the cospan graph \(\boxed{\overset{x}\bullet \xrightarrow{f} \overset{a}\bullet \xleftarrow{g}\overset{y}\bullet}\) then its limit is known as a pullback.
Given the diagram \(X \xrightarrow{f}A\xleftarrow{g}Y\), the pullback is the cone shown below:
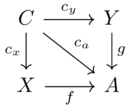
Because the diagram commutes, the diagonal arrow is superfluous. One can denote pullbacks instead like so:
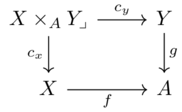
The pullback picks out the \((X,Y)\) pairs which map to the same output.